Мощным средством исследования в математике, физике, механике и других дисциплинах является определенный интеграл – одно из основных понятий математического анализа. Геометрический смысл интеграла – площадь криволинейной трапеции. Физический смысл интеграла – 1) масса неоднородного стержня с плотностью, 2) перемещение точки, движущейся по прямой со скоростью за промежуток времени.
Напомню свойства интеграла:
Как вычислять площадь криволинейной трапеции мы уже тренировались. Вычисление объемов тел хорошо разобрано в учебнике на стр.194 и 195.
А вот физическое приложение интегралов покажу подробнее.
Путь, пройденный точкой при неравномерном движении по прямой с переменной скоростью  за промежуток времени от
за промежуток времени от 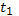 до
до 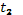 вычисляется по формуле
вычисляется по формуле 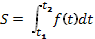 .
.
1. Скорость движения точки 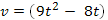 м/с. Найти путь, пройденный точкой за 4-ю секунду.
м/с. Найти путь, пройденный точкой за 4-ю секунду.
Решение: согласно условию,  . Следовательно,
. Следовательно, 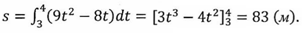
2. Два тела начали двигаться одновременно из одной точки в одном направлении по прямой. Первое тело движется со скоростью 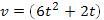 м/с, второе — со скоростью v = (4t+5) м/с. На каком расстоянии друг от друга они окажутся через 5 с?
м/с, второе — со скоростью v = (4t+5) м/с. На каком расстоянии друг от друга они окажутся через 5 с?
Решение: очевидно, что искомая величина есть разность расстояний, пройденных первым и вторым телом за 5 с:
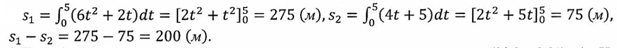
3. Тело брошено с поверхности земли вертикально вверх со скоростью и = (39,2—9,8^) м/с. Найти наибольшую высоту подъема тела.
Решение: тело достигнет наибольшей высоты подъема в такой момент времени t, когда v = 0, т.е. 39,2—9,8t = 0, откуда I = 4 с. По формуле (1) на ходим

2. ВЫЧИСЛЕНИЕ РАБОТЫ СИЛЫ
Работа, произведенная переменной силой f(х) при перемещении по оси Ох материальной точки от х = а до х=b, находится по формуле 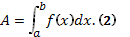 При решении задач на вычисление работы силы часто используется закон Г у к а: F=kx, (3) где F — сила Н; х—абсолютное удлинение пружины, м, вызванное силой F, а k —коэффициент пропорциональности, Н/м.
При решении задач на вычисление работы силы часто используется закон Г у к а: F=kx, (3) где F — сила Н; х—абсолютное удлинение пружины, м, вызванное силой F, а k —коэффициент пропорциональности, Н/м.
1. Пружина в спокойном состоянии имеет длину 0,2 м. Сила в 50 Н растягивает пружину на 0,01 м. Какую работу надо совершить, чтобы растянуть ее от 0,22 до 0,32 м?
Решение: используя равенство (3), имеем 50=0,01k, т. е. kК = 5000 Н/м. Находим пределы интегрирования: а = 0,22 — 0,2 = 0,02 (м), b=0,32— 0,2 = 0,12(м). Теперь по формуле (2) получим
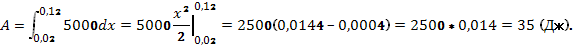
3. ВЫЧИСЛЕНИЕ РАБОТЫ, ПРОИЗВОДИМОЙ ПРИ ПОДНЯТИИ ГРУЗА
Задача. Цилиндрическая цистерна с радиусом основания 0,5 м и высотой 2 м заполнена водой. Вычислить работу, которую необходимо произвести, чтобы выкачать воду из цистерны.
Решение: выделим на глубине х горизонтальный слой высотой dх (рис.). Работа А, которую надо произвести, чтобы поднять слой воды весом Р на высоту х, равна Рх.
Изменение глубины х на малую величину dх вызовет изменение объема V на величину dV = пr 2 dх и изменение веса Р на величину * dР = 9807 r 2 dх; при этом совершаемая работа А изменится на величину dА=9807пr 2 хdх. Проинтегрировав это равенство при изменении x от 0 до Н, получим
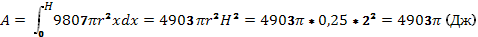
4. ВЫЧИСЛЕНИЕ СИЛЫ ДАВЛЕНИЯ ЖИДКОСТИ
Значение силы Р давления жидкости на горизонтальную площадку зависит от глубины погружения х этой площадки, т. е. от расстояния площадки до поверхности жидкости.
Сила давления (Н) на горизонтальную площадку вычисляется по формуле Р =9807 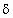 S x,
S x,
где 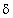 — плотность жидкости, кг/м 3 ; S — площадь площадки, м 2 ; х — глубина погружения площадки, м.
— плотность жидкости, кг/м 3 ; S — площадь площадки, м 2 ; х — глубина погружения площадки, м.
Если площадка, испытывающая давление жидкости, не горизонтальна, то давление на нее различно на разных глубинах, следовательно, сила давления на площадку есть функция глубины ее погружения Р (х).
5. ДЛИНА ДУГИ
Пусть плоская кривая АВ (рис. ) задана уравнением у =f(x) (a 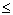 x
x 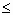 b), причем f(x) и f ?(x) — непрерывные функции в промежутке [а,b]. Тогда дифференциал dl длины дуги АВ выражается формулой
b), причем f(x) и f ?(x) — непрерывные функции в промежутке [а,b]. Тогда дифференциал dl длины дуги АВ выражается формулой 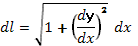 или
или 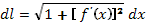 , а длина дуги АВ вычисляется по формуле
, а длина дуги АВ вычисляется по формуле 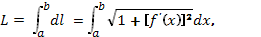 (4)
(4)
где а и b—значения независимой переменной х в точках А и В. Если кривая задана уравнением х = 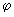 (у)(с у
(у)(с у 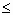 d), то длина дуги АВ вычисляется по формуле
d), то длина дуги АВ вычисляется по формуле 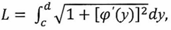 (5) где с и д значения независимой переменной у в точках А и В.
(5) где с и д значения независимой переменной у в точках А и В.
6. ЦЕНТР МАСС
При нахождении центра масс пользуются следующими правилами:
1) Координата х? центра масс системы материальных точек А1, А2 . Аn с массами m1, m2, . mn, расположенных на прямой в точках с координатами х1, х2, . хn, находятся по формуле
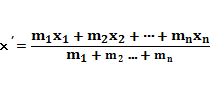 (*); 2) При вычислении координаты центра масс можно любую часть фигуры заменить на материальную точку, поместив ее в центр масс этой части, и приписать ей массу, равную массе рассматриваемой части фигуры. Пример. Пусть вдоль стержня-отрезка [а;b] оси Ох — распределена масса плотностью
(*); 2) При вычислении координаты центра масс можно любую часть фигуры заменить на материальную точку, поместив ее в центр масс этой части, и приписать ей массу, равную массе рассматриваемой части фигуры. Пример. Пусть вдоль стержня-отрезка [а;b] оси Ох — распределена масса плотностью 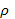 (х), где
(х), где 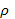 (х) — непрерывная функция. Покажем, что а) суммарная масса М стержня равна
(х) — непрерывная функция. Покажем, что а) суммарная масса М стержня равна 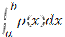 ; б) координата центра масс х‘ равна
; б) координата центра масс х‘ равна 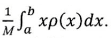 .
.
Разобьем отрезок [а; b] на n равных частей точками а= х 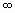 числитель стремится к интегралу
числитель стремится к интегралу 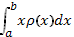 , а знаменатель (выражающий массу всего стержня) — к интегралу
, а знаменатель (выражающий массу всего стержня) — к интегралу 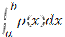 .
.
Разделы: Математика
Девиз урока: “Математика – язык, на котором говорят все точные науки” Н.И. Лобачевский
Цель урока: обобщить знания учащихся по теме “Интеграл”, “Применение интеграла”;расширить кругозор, знания о возможном применении интеграла к вычислению различных величин; закрепить навыки использовать интеграл для решения прикладных задач; прививать познавательный интерес к математике, развивать культуру общения и культуру математической речи; уметь учиться выступать перед учащимися и учителями.
Тип урока: повторительно-обобщающий.
Вид урока: урок – защита проекта “Применение интеграла”.
Оборудование: магнитная доска, плакаты “Применение интеграла”, карточки с формулами и заданиями для самостоятельной работы.
1. Защита проекта:
- из истории интегрального исчисления;
- свойства интеграла;
- применение интеграла в математике;
- применение интеграла в физике;
2. Решение упражнений.
Ход урока
Учитель: Мощным средством исследования в математике, физике, механике и других дисциплинах является определенный интеграл – одно из основных понятий математического анализа. Геометрический смысл интеграла – площадь криволинейной трапеции. Физический смысл интеграла – 1) масса неоднородного стержня с плотностью, 2) перемещение точки, движущейся по прямой со скоростью за промежуток времени.
Учитель: Ребята нашего класса провели большую работу, они подобрали задачи, где применяется определенный интеграл. Им слово.
2 ученик: Свойства интеграла
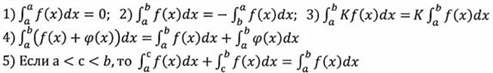
3 ученик: Применение интеграла (на магнитной доске таблица).
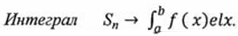 при
при 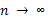 .
.
4 ученик: Рассматриваем применение интеграла в математике для вычисления площади фигур.
Площадь всякой плоской фигуры, рассматриваемая в прямоугольной системе координат, может быть составлена из площадей криволинейных трапеций, прилежащих к оси Ох и оси Оу. Площадь криволинейной трапеции, ограниченной кривой у = f(х), осью Ох и двумя прямыми х=а и х=b, где а 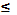 х
х 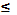 b, f(х)
b, f(х) 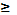 вычисляется по формуле
вычисляется по формуле 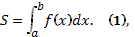 см. рис. Если криволинейная трапеция прилегает к оси Оу, то её площадь вычисляется по формуле
см. рис. Если криволинейная трапеция прилегает к оси Оу, то её площадь вычисляется по формуле  , см. рис. При вычислении площадей фигур могут представиться следующие случаи: а)Фигура расположена над осью Ох и ограничена осью Ох, кривой у=f(х) и двумя прямыми х=а и х=b.(См. рис.) Площадь этой фигуры находится по формуле 1 или 2. б) Фигура расположена под осью Ох и ограничена осью Ох, кривой у=f(х) и двумя прямыми х=а и х=b (см. рис.). Площадь находится по формуле
, см. рис. При вычислении площадей фигур могут представиться следующие случаи: а)Фигура расположена над осью Ох и ограничена осью Ох, кривой у=f(х) и двумя прямыми х=а и х=b.(См. рис.) Площадь этой фигуры находится по формуле 1 или 2. б) Фигура расположена под осью Ох и ограничена осью Ох, кривой у=f(х) и двумя прямыми х=а и х=b (см. рис.). Площадь находится по формуле 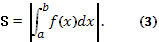 . в) Фигура расположена над и под осью Ох и ограничена осью Ох, кривой у=f(х) и двумя прямыми х=а и х=b(рис. ). г) Площадь ограничена двумя пересекающимися кривыми у=f(х) и у =
. в) Фигура расположена над и под осью Ох и ограничена осью Ох, кривой у=f(х) и двумя прямыми х=а и х=b(рис. ). г) Площадь ограничена двумя пересекающимися кривыми у=f(х) и у =  (х) (рис.)
(х) (рис.)
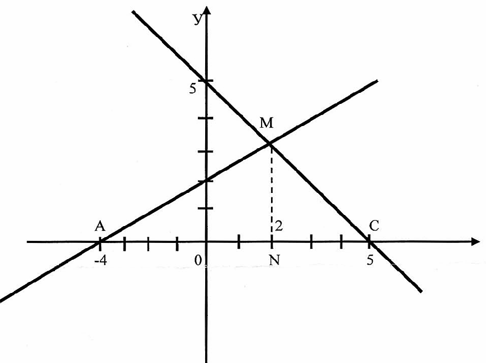
5 ученик: Решим задачу
х-2у+4=0 и х+у-5+0 и у=0
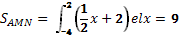
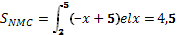
7 ученик: Интеграл, широко применяющийся в физике. Слово физикам.
1. ВЫЧИСЛЕНИЕ ПУТИ, ПРОЙДЕННОГО ТОЧКОЙ
Путь, пройденный точкой при неравномерном движении по прямой с переменной скоростью 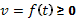 за промежуток времени от
за промежуток времени от 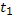 до
до 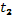 вычисляется по формуле
вычисляется по формуле 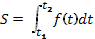 .
.
1. Скорость движения точки 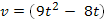 м/с. Найти путь, пройденный точкой за 4-ю секунду.
м/с. Найти путь, пройденный точкой за 4-ю секунду.
Решение: согласно условию,  . Следовательно,
. Следовательно, 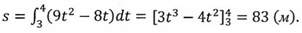
2. Два тела начали двигаться одновременно из одной точки в одном направлении по прямой. Первое тело движется со скоростью 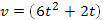 м/с, второе — со скоростью v = (4t+5) м/с. На каком расстоянии друг от друга они окажутся через 5 с?
м/с, второе — со скоростью v = (4t+5) м/с. На каком расстоянии друг от друга они окажутся через 5 с?
Решение: очевидно, что искомая величина есть разность расстояний, пройденных первым и вторым телом за 5 с:
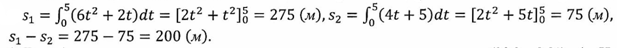
3. Тело брошено с поверхности земли вертикально вверх со скоростью и = (39,2—9,8^) м/с. Найти наибольшую высоту подъема тела.
Решение: тело достигнет наибольшей высоты подъема в такой момент времени t, когда v = 0, т.е. 39,2—9,8t = 0, откуда I = 4 с. По формуле (1) на ходим

2. ВЫЧИСЛЕНИЕ РАБОТЫ СИЛЫ
Работа, произведенная переменной силой f(х) при перемещении по оси Ох материальной точки от х = а до х=b, находится по формуле 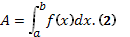 При решении задач на вычисление работы силы часто используется закон Г у к а: F=kx, (3) где F — сила Н; х—абсолютное удлинение пружины, м, вызванное силой F, а k —коэффициент пропорциональности, Н/м.
При решении задач на вычисление работы силы часто используется закон Г у к а: F=kx, (3) где F — сила Н; х—абсолютное удлинение пружины, м, вызванное силой F, а k —коэффициент пропорциональности, Н/м.
1. Пружина в спокойном состоянии имеет длину 0,2 м. Сила в 50 Н растягивает пружину на 0,01 м. Какую работу надо совершить, чтобы растянуть ее от 0,22 до 0,32 м?
Решение: используя равенство (3), имеем 50=0,01k, т. е. kК = 5000 Н/м. Находим пределы интегрирования: а = 0,22 — 0,2 = 0,02 (м), b=0,32— 0,2 = 0,12(м). Теперь по формуле (2) получим
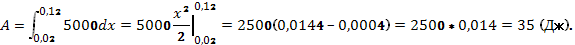
3. ВЫЧИСЛЕНИЕ РАБОТЫ, ПРОИЗВОДИМОЙ ПРИ ПОДНЯТИИ ГРУЗА
Задача. Цилиндрическая цистерна с радиусом основания 0,5 м и высотой 2 м заполнена водой. Вычислить работу, которую необходимо произвести, чтобы выкачать воду из цистерны.
Решение: выделим на глубине х горизонтальный слой высотой dх (рис.). Работа А, которую надо произвести, чтобы поднять слой воды весом Р на высоту х, равна Рх.
Изменение глубины х на малую величину dх вызовет изменение объема V на величину dV = пr 2 dх и изменение веса Р на величину * dР = 9807 r 2 dх; при этом совершаемая работа А изменится на величину dА=9807пr 2 хdх. Проинтегрировав это равенство при изменении x от 0 до Н, получим
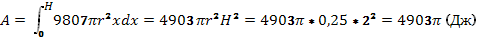
4. ВЫЧИСЛЕНИЕ СИЛЫ ДАВЛЕНИЯ ЖИДКОСТИ
Значение силы Р давления жидкости на горизонтальную площадку зависит от глубины погружения х этой площадки, т. е. от расстояния площадки до поверхности жидкости.
Сила давления (Н) на горизонтальную площадку вычисляется по формуле Р =9807 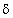 S x,
S x,
где 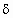 — плотность жидкости, кг/м 3 ; S — площадь площадки, м 2 ; х — глубина погружения площадки, м.
— плотность жидкости, кг/м 3 ; S — площадь площадки, м 2 ; х — глубина погружения площадки, м.
Если площадка, испытывающая давление жидкости, не горизонтальна, то давление на нее различно на разных глубинах, следовательно, сила давления на площадку есть функция глубины ее погружения Р (х).
5. ДЛИНА ДУГИ
Пусть плоская кривая АВ (рис. ) задана уравнением у =f(x) (a 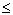 x
x 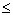 b), причем f(x) и f ?(x) — непрерывные функции в промежутке [а,b]. Тогда дифференциал dl длины дуги АВ выражается формулой
b), причем f(x) и f ?(x) — непрерывные функции в промежутке [а,b]. Тогда дифференциал dl длины дуги АВ выражается формулой 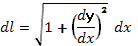 или
или 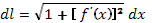 , а длина дуги АВ вычисляется по формуле
, а длина дуги АВ вычисляется по формуле 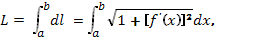 (4)
(4)
где а и b—значения независимой переменной х в точках А и В. Если кривая задана уравнением х = 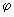 (у)(с у
(у)(с у 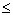 d), то длина дуги АВ вычисляется по формуле
d), то длина дуги АВ вычисляется по формуле 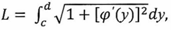 (5) где с и д значения независимой переменной у в точках А и В.
(5) где с и д значения независимой переменной у в точках А и В.
6. ЦЕНТР МАСС
При нахождении центра масс пользуются следующими правилами:
1) Координата х? центра масс системы материальных точек А1, А2 . Аn с массами m1, m2, . mn, расположенных на прямой в точках с координатами х1, х2, . хn, находятся по формуле
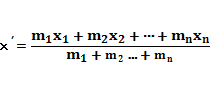 (*); 2) При вычислении координаты центра масс можно любую часть фигуры заменить на материальную точку, поместив ее в центр масс этой части, и приписать ей массу, равную массе рассматриваемой части фигуры. Пример. Пусть вдоль стержня-отрезка [а;b] оси Ох — распределена масса плотностью
(*); 2) При вычислении координаты центра масс можно любую часть фигуры заменить на материальную точку, поместив ее в центр масс этой части, и приписать ей массу, равную массе рассматриваемой части фигуры. Пример. Пусть вдоль стержня-отрезка [а;b] оси Ох — распределена масса плотностью 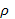 (х), где
(х), где 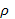 (х) — непрерывная функция. Покажем, что а) суммарная масса М стержня равна
(х) — непрерывная функция. Покажем, что а) суммарная масса М стержня равна 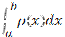 ; б) координата центра масс х‘ равна
; б) координата центра масс х‘ равна 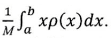 .
.
Разобьем отрезок [а; b] на n равных частей точками а= х 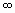 числитель стремится к интегралу
числитель стремится к интегралу 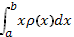 , а знаменатель (выражающий массу всего стержня) — к интегралу
, а знаменатель (выражающий массу всего стержня) — к интегралу 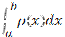
Для нахождения координат центра масс системы материальных точек на плоскости или в пространстве также пользуются формулой(*)
Учитель: У вас на столах таблица и задачи, используя таблицу найдите: а) количество электричества; б) массу стержня по его плотности.
Величины
Вычисление производной
Вычисление интеграла
N — мощность.
N(t)=A’ (t).
A=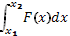 ;
;
A=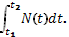
m –масса тонкого стержня
p – линейная плотность
P(x)=m’ (x).
m=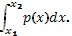
Q –электрический заряд;
I – сила тока.
I(t)=q’ (t)
Q=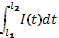
v –скорость.
V(t)=S’ (t)
S=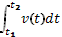
Q –количество теплоты;
с – теплоёмкость.
C(t)=Q’ (t)
Q=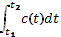
Физические приложения интеграла
Вариант 1
Вариант 2
- Вычислите массу участка стержня от
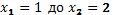 , если его линейная плотность задается формулой
, если его линейная плотность задается формулой 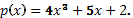
- Вычислите работу за промежуток времени [4;9 ], если мощность вычисляется по формуле
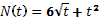 /
/
- Вычислите количество электричества, протекшего по проводнику за промежуток времени [ 2;3 ], если сила тока задается формулой
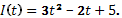
- Вычислите работу по переносу единичной массы, совершенную силой
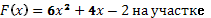 [ -1;2].
[ -1;2].
Итог урока: Завершили тему “Интеграл”, научились вычислять первообразные, интегралы, площади фигур, рассмотрели применение интеграла на практике, данные задачи могут встретиться на ЕГЭ, думаю, с ними вы справитесь.
Геометрический смысл определенного интеграла как площади криволинейной трапеции дает возможность применить его к вычислению любых площадей. Однако определенный интеграл в интервале  далеко не всегда дает значение площади как физической величины, измеряемой в квадратных единицах. Необходимо учесть, что геометрический смысл построен на формальном приписывании знаков: части функции над осью оХ (и площадь под ними) принимаются со знаком "плюс", а части функции под осью оХ (и площадь над ними) берутся со знаком "минус". Очевидно, что если поставить задачу о вычислении собственно площадей, то обязательно следует учесть строгую положительность понятия площади как физической величины. Чтобы полностью разобраться с разницей между геометрическим смыслом интеграла и площадью, рассмотрим пример: вычислить интеграл
далеко не всегда дает значение площади как физической величины, измеряемой в квадратных единицах. Необходимо учесть, что геометрический смысл построен на формальном приписывании знаков: части функции над осью оХ (и площадь под ними) принимаются со знаком "плюс", а части функции под осью оХ (и площадь над ними) берутся со знаком "минус". Очевидно, что если поставить задачу о вычислении собственно площадей, то обязательно следует учесть строгую положительность понятия площади как физической величины. Чтобы полностью разобраться с разницей между геометрическим смыслом интеграла и площадью, рассмотрим пример: вычислить интеграл 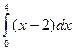 и площадь, которую ограничивает подынтегральная функция.
и площадь, которую ограничивает подынтегральная функция.
1. Вычислим интеграл:  . 2. По геометрическому смыслу интеграл является алгебраической суммой площадей нижнего и верхнего треугольников, т.е. . 2. По геометрическому смыслу интеграл является алгебраической суммой площадей нижнего и верхнего треугольников, т.е.  |
Нарисуем эскиз расчетной области и проведем вычисления по пунктам:
 |
Как и следовало ожидать, результаты совпали. Подсчитаем площадь.
3.  квадратных единиц.
квадратных единиц.
Здесь знак модуля обеспечивает безусловную положительность результатов и соответствие физическому смыслу. Таким образом, общая формула для вычисления площади с применением определенного интеграла будет иметь вид
 ,
,
где  — число подинтервалов, на которые разбивается площадь под кривой
— число подинтервалов, на которые разбивается площадь под кривой 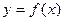 ;
; 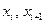 — абсциссы начала и конца подинтервала.
— абсциссы начала и конца подинтервала.
Определение площади следует производить в два этапа. На первом решается уравнение  и находится число подинтервалов. На втором этапе применяется формула площади. Рекомендуется выполнить эскиз расчетной области. В трудных случаях можно использовать графическое разложение сложной фигуры на сумму более простых.
и находится число подинтервалов. На втором этапе применяется формула площади. Рекомендуется выполнить эскиз расчетной области. В трудных случаях можно использовать графическое разложение сложной фигуры на сумму более простых.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9155 —  | 7236 —
| 7236 —  или читать все.
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно

